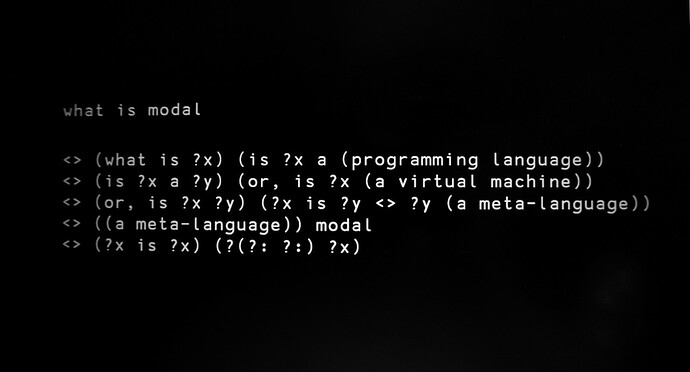
Hi,
I’d like to show you a language by wryl that I’ve enjoyed learning these past few weeks, and that might be of interest to you all. It’s relevant to Malleable systems as it’s a very small runtime(200 lines of C), capable of hosting a pretty capable system.
It’s a string-rewriting programming language, and meta-language(a language to define other languages) that has one operation, replace left with right.
Modal on a postcard.
Basics
To define a new rule, start with <>, followed by a left and a right statement, which is either a word, or a tree. The program evaluation starts at the first character of the string and walks through to the end trying to match a transformation rule from that location:
Registers are single-character identifiers bound to an address in a pattern used in rewriting:
<> (copy ?a) (?a ?a)
.. copy cat
00 cat cat
When a register is used in a pattern, and when we try to match a given tree with a pattern, each register is bound to a corresponding an address and referenced in either side of a rule:
<> (swap ?x ?y) (?y ?x)
.. (swap fox rat)
00 (rat fox)
When a register appears more than once in a rule, each instance is bound to the first address:
<> (?x ?x ?x) triplet
.. (fox fox fox)
00 (triplet)
Trees can be found in rules and program data, they include words, registers and nested trees. Rules can match specific trees and rewrite their content in a new sequence.
<> (rotate ?x (?y) ?z) (?y (?z) ?x)
.. rotate foo (bar) baz
00 bar (baz) foo
An efficient way to represent an array is to store information in nested lists, it allows for rules to target specific segments of the list, similarly to Lisp’s car and cdr primitives. To print each element of such a structure, we can use the following recursive rules:
<> (putrec (?: ?x)) (putrec ?:?x)
<> ((putrec (?:))) (?:)
.. (putrec (a (b (c (d (e))))))
00 (putrec (b (c (d (e)))))
00 (putrec (c (d (e))))
00 (putrec (d (e)))
00 (putrec (e))
01
Understanding how to use types to guard rules for specific evaluation order is important to become proficient with Modal. Creating a type system is merely a matter of creating stricter rules expecting a specific grammar.
<> (join ?^) (?^)
<> (join-strings (String ?x) (String ?y)) (join (?x ?y))
.. join-strings (String foo) (String bar)
01 join (foo bar)
00 foobar
Let us build a logic system, starting by comparing two registers:
<> (eq ?x ?x) (#t)
<> (eq ?x ?y) (#f)
.. (eq fox bat)
01 (#f)
We can implement the truth tables by defining each case:
<> (and #t #t) #t <> (or #t #t) #t
<> (and #t #f) #f <> (or #t #f) #t
<> (and #f #t) #f <> (or #f #t) #t
<> (and #f #f) #f <> (or #f #f) #f
<> (not #t) #f <> (not #f) #t
.. (or #f #t)
08 (#t)
Building on the comparison rule above, we can write conditionals with a ternary statement:
<> (ife #t ?t ?f) (?t)
<> (ife #f ?t ?f) (?f)
<> (print ?:) (?:)
.. ife #f (print True!) (print False!)
13 (print False!)
14 ()
So, what
Turns out loads of things can be implemented in a simple string-rewriting scheme without too much fussing, like tic-tac-toe. I’m currently implementing a little game of mine called Paradise in it, and I’m only scratching the surface.
Some things are surprisingly easy to implement, like combinator calculus:
<> (M ?x) (?x ?x)
<> (KI ?x ?y) (?y)
<> (T ?x ?y) (?y ?y)
<> (W ?x ?y) (?x ?y ?y)
<> (K ?x ?y) (?x)
<> (C ?x ?y ?z) (?x ?z ?y)
<> (B ?x ?y ?z) (?x (?y ?z))
<> (I ?x) (?x)
<> (S ?x ?y ?z) (?x ?z (?y ?z))
.. C KI x y z
05 KI y x z
01 x z
Or, a concatenative stack machine:
<> (?x dup) (?x ?x)
<> (?x ?y swap) (?y ?x)
<> (?x pop) ()
.. (1 2 3) (4 5 6) swap pop dup
01 (4 5 6) (1 2 3) pop dup
02 (4 5 6) dup
00 (4 5 6) (4 5 6)
Well, I hope that will make you look into string-rewriting programming, it’s a paradigm that’s mostly unknown but endless fun to use.
Have a good one ![]()